【ｔ検定】初心者でも簡単！エクセルでの平均データの検証方法を解説【関数のみ】

 

この記事では、平均データを比較する際にその数値が「偶然出た数値」か、または「意味のある数値」かを検証する「ｔ検定」についてエクセルで行う方法を解説していきます。

この記事を読むとエクセルで「ｔ検定」をつかって、データの検証を行うことができるようになるので、データに説得力を持たすことができます。

データの検証を行うには統計的手法である「ｔ検定」を行います。

「統計」という文字をみると非常に難しく感じてしまいますが、

エクセルを使うと高度な数学の知識などを用いなくても、とても簡単に「ｔ検定」を行うことができます。

ｔ検定とは

まず、ｔ検定とはなにかについて解説します。

私は工場の品質管理をしていたことがありました。

そのとき、試作品Aと試作品Bで試験を行い製品の特性値を調べるのですが、

試作品Aと試作品Bであきらかに差があるときはいいです。

しかし、データもバラついて、試験回数もそれほど多く取れない時に、試作品Aと試作品Bの間で特性値の平均値が微妙に差があったときに、

これを「差がある」と報告していいものかどうか、よく悩みました。

ｔ検定とはこういった微妙なデータが統計的に見て、

「差がある」とか

「Aの方が高いです」、

「Bの方が低いです」という根拠になる指針です。

データをとるのが1回きりでそれで、どちらの数値が高かったのかの比較をする場合や、

ケタが違うといったあきらかな結果がでれば簡単なのですが、

A組とＢ組といったように、データが「グループ」で存在して、差があるが、それほど大きな差ではないといった場合はどうでしょうか？

とりあえずデータの平均をだして、AとＢを比較することが多いと思いますが、

実はこれだけではデータを正確に検証することはできません。

データには「バラつき」というものが存在するからです。

例えば、製品のAとBで製品の強度を測定して比較したとします。

1回目の測定結果が

製品Aが10.2

製品Bが9.5

となりました。

この結果をみると製品Aの方が製品Bよりも強度が高いと言えます。

しかし、2回目の測定を行った場合、

製品Aが9.8

製品Bが10.3

と測定結果がでたとしたらどうでしょうか？

今度は、製品Ｂの方が製品Aよりも強度が高いと言えます。

この測定を10回繰り返したとして、

その10回の平均が

製品Aの平均が10.3

製品Bが9.7

であったとします。

こんどこそ、製品Aの方が製品Bよりも強度が高いと言えるでしょうか？

データを比較したいときには、単純に平均を比較するだけでは不十分です。

「バラつき」を加味して比較をしなくてはいけません。

この時に、使用するのが「ｔ検定」です。

ｔ検定をもちいることで、A組、Ｂ組といった2グループのデータの比較が統計的に見て正しいかどうか（意味のある数字かどうか）を調べることができます。

ｔ検定の種類

ｔ検定には以下の3種類があります。

①同対象の検定

ある製品の「めっき処理する前を特性値」と「処理後を特性値」やA組の100m走の1回目と2回目のタイムといった「同じ対象を、異なった条件で測定して、その違いをみる」といった場合には「同対象の検定」を使います。

②Studentの検定

製品Aと製品Ｂの特性値といった「別の対象を、同じ条件で測定して、その違いを見る」といった場合でバラつき、つまりバラつきは同じといった場合はこの「Studentの検定」を行います。

③Welchの検定

製品Aと製品Ｂの特性値といった「違う対象を、同じ条件で測定して、その違いを見る」といった場合で「バラつきも違う」といった場合はこの「Welchの検定」を行います。

それではエクセルでｔ検定を行う方法を見ていきましょう 

エクセルでの平均値の検証方法【①同対象の検定】

エクセルでｔ検定を行う方法がとても簡単です。

任意のセルに

＝Ｔ.TEST(データの範囲A,データの範囲Ｂ,検定の指定,検定の種類)

と入力していくだけです。

サンプルでは、商品Aを2回試験して、1回目の平均6.3、2回目の平均5.9と試験結果が出ていますが、この結果で「2回目の平均は1回目よりも低い」と検証していいかを調べていきます。 

セルに

＝T.TEST(C6:C15,D6:D15,1,1)と入力します。

検定の指定は

1：片側の分布

2：両側の分布

となっていて、低いか、高いかを検証する場合は1を選択します。

検定の種類は上述したｔ検定の3つの種類です。

1：対応のある検定

2：対応はないが、バラつきは同じデータの検定

3：対応も、バラつきも違うデータの検定

です。今回は1を選びましょう。 

ENTERを押すと、関数の結果が表示されます。

この数値が「0.05」未満であれば、この平均値は低いとみなしてよいと考えられます。

なので、このサンプルでは2回目の結果はたまたまではなく、統計的に意味があるとみていいということです。

この0.05はｐ値と呼ばれるもので、関数を用いて見る場合は0.05の固定で考えてOKです。

0.05 ＜ ｐ ：偶然で起きた、バラつきの範囲の結果

0.05 ＞ ｐ ：偶然ではなく、きちんとした意味のある結果

となります。 

試しに、赤く囲った2つのデータを変えてみましょう。

結果は1回目6.3、2回目6.0とまだ、2回目のデータの方が平均値は低いですが、

ｐ値は0.097と0.05よりずいぶんと大きくなってしまいました。

この結果から、2回目の6.0という結果はたまたま低くでただけと考えられます。

このデータのでかたでは、測定を10回ですが、20回、30回と増やしていくと、平均値が逆転してしまう可能性があるわけです。 

エクセルでの平均データの検証方法【②Studentのt検定】

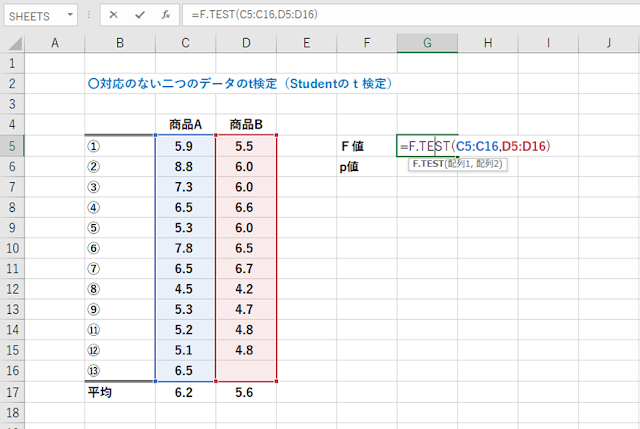
次は、商品Aと商品Ｂの特性値を比較してみます。

違う商品で、測定回数も違うデータです。

商品Aは6.2、商品Bは5.6とあきらかに商品Bの方が平均値は低いですが、商品Bの方が測定回数も少ないので、何とも言えません。 

まず、バラつきに差がないかを見てみましょう。

バラつきに差が無いかを見るには、Ｆ検定を行います。

Ｆ検定は任意のセルに

F.TEST（データ範囲A,データ範囲B）と入力するだけです。

これで、2つのデータのバラつきに差あるかを見ることができます。

この数値をＦ値というのですが、この数値が0.05より大きければバラつきに差はない、

つまり、バラつきは同じくらいとみなせます。 

結果は0.248でしたので、バラつきの差はない考えていいです。 

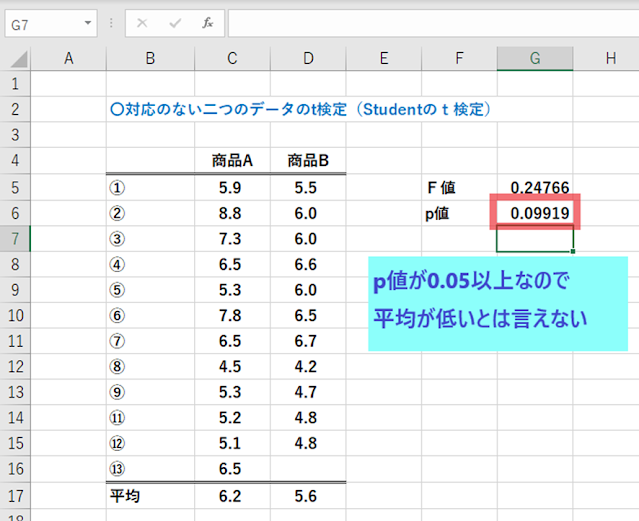
つぎに先ほどと同様に、ｔ検定を行っていきます。

＝T.TEST(C6:C15,D6:D15,1,2)と入力します。 

結果をみると0.099と0.05より高い値がでました。

これで、商品Aと商品Bの平均値の間に有意性はないとみなされるので、

「平均値は低いけど、一概に商品Ｂの特性値の方が低い」とは言えないということになります。 

エクセルでの平均値の検証方法【③Welchのt検定】

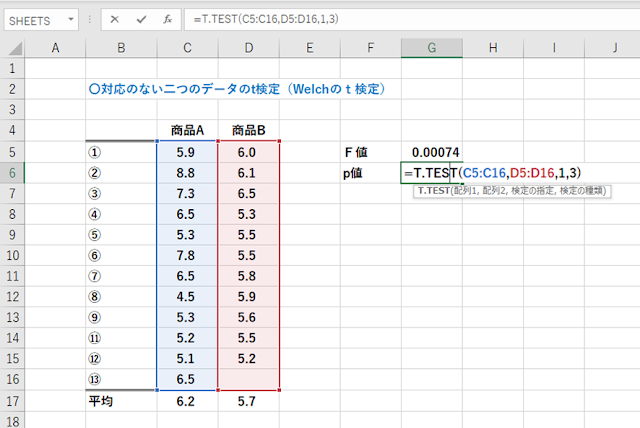
最後に「③データの対応も、バラつきも違うデータの検定」について説明します。

サンプルでは先ほどと同様に商品Aと商品Ｂの特性値があり、商品Aの平均は6.2、商品Bの平均は5.7とあります。

先程と違うのは、商品Bの測定結果のバラつきが低いという事です。 

Ｆ検定を行ってみましょう。

検定の結果は0.00074と0.05より低いので、この二つのデータのバラつきは違うということになります。 

＝T.TEST(C6:C15,D6:D15,1,3)と入力します。 

結果はｐ値が0.104と0.05より大きいので、「たまたまであり、バラつきの範囲の結果」となりました。

商品Bの方が特性値が低いとは一概には言えないということですね。 

まとめ

データの比較したいときには、t検定を行い、結果のp値を見ましょう。

結果が「0.05 ＞ ｐ」であれば、データは違うと考えていい。

結果が「0.05 ＜ ｐ」であれば、たまたま、その数値になっただけで、試験を続けていくと違う結果になるかもしれないよという事になります。